Wprowadzenie do przetwarzania obrazów

Politechnika Poznańska, Instytut Robotyki i Inteligencji Maszynowej

Ćwiczenie laboratoryjne 4: Przekształcenia geometryczne

Powrót do spisu treści ćwiczeń laboratoryjnych

Obsługa myszy i rysowanie figur na obrazie

W celu obsługi myszy niezbędne jest “podpięcie” funkcji jej obsługi (tzw. callbacku) do odpowiedniego okna. Jest to realizowane za pomocą funkcji setMouseCallback (dokumentacja). Wymagany format tej funkcji wygląda następująco: MouseCallback(event, x, y, flags, userdata). Zdarzenia oraz flagi związane z obsługą myszki znajdziesz w https://docs.opencv.org/5.x/d0/d90/group__highgui__window__flags.html.

W momencie wystąpienia zdarzenia (tj. naciśnięcia jednego z przycisków myszy, lub klawisza CTRL, SHIFT lub ALT) wywołana będzie podpięta funkcja, której argumenty zostaną przez system automatycznie uzupełnione (tj. przekazana będzie aktualna położenie kursora na obrazie, a wszystkie flagi przyjmą odpowiednie wartości). Własne dane do funkcji obsługi zdarzenia można przekazać jako argument userdata.

💥 Zadanie do wykonania 💥

Napisz program rysujący kwadrat po naciśnięciu lewego klawisza myszy oraz okrąg po naciśnięciu prawego. Wykorzystaj do tego celu funkcję cv2.circle oraz cv2.rectangle (dokumentacja), wykorzystując do tego celu współrzędne kursora myszy i przykładowy kod dostępny w https://docs.opencv.org/5.x/db/d5b/tutorial_py_mouse_handling.html.

Uwaga:
W systemie Ubuntu pod prawym przyciskiem myszy kryje się menu kontekstowe. Z tego powodu należy kliknąć prawy przycisk dwukrotnie lub wykorzystać środkowy przycisk myszy.

Transformacje geometryczne

Oprócz poznanej na ostatnich zajęciach operacji skalowania w OpenCV dostępne są również inne transformacje geometryczne takie jak translacja (przesunięcie), czy rotacja (obrót).

• Translacja

  Translacja o wektor \(t_x\), \(t_y\) jest realizowana przekształceniem: \[ R=\begin{bmatrix} 0 & 0 & t_{x} \\\\ 0 & 0 & t_{y} \\\\ 0 & 0 & 1 \end{bmatrix} \]

• Rotacja

  Rotacja o kąt jest realizowana za pomocą macierzy: \[ R=\begin{bmatrix} cos(\theta) & -sin(\theta) & 0 \\\\ sin(\theta) & cos(\theta) & 0 \\\\ 0 & 0 & 1 \end{bmatrix} \]

Oba te przekształcenia oraz skalowanie są szczególnymi przypadkami (elementami) transformacji afinicznej. Jej cechą jest zachowanie równoległości - linie równoległe pozostają równoległe również po zastosowaniu przekształcenia.

• Transformacje afiniczne

  Transformacja afiniczna przekształca współrzędne poszczególnych pikseli obrazu we współrzędne innego, liniowo zależnego układu współrzędnych. Transformacja zachowuje równoległość prostych, tj. punkty, które leżały na jednej prostej po przekształceniu nadal leżą na jednej prostej, a dodatkowo zachowany jest stosunek odległości (środek odcinka pozostaje środkiem danego odcinka po przekształceniu).

  Transformacje afiniczne realizowane są przez przemnożenie dotychczasowych współrzędnych (przedstawionych jako współrzędne jednorodne) przez macierz przekształcenia R o wymiarach 3x3: \[ \begin{bmatrix}x'\\\\ y'\\\\ 1\end{bmatrix}=R\begin{bmatrix} x\\\\ y\\\\ 1\end{bmatrix} \]

• Transformacje perspektywiczna

  Transformacja perspektywiczna przekształca dowolny czworokąt w jednej płaszczyźnie na czworokąt określony w innej płaszczyźnie. Transformacja ta zachowuje linie proste, lecz może zmieniać kąty między nimi. Efekty przekształceń można zaobserwować w podanych przykładach. Transformacja realizowana jest za pomocą mnożenia przez macierz R o wymiarach 3x3:

  \[ \begin{bmatrix} \omega{x}'\\\\ \omega{y}'\\\\ \omega \end{bmatrix}=R\begin{bmatrix} x\\\\ y\\\\ 1 \end{bmatrix} \]

  gdzie macierz przekształcenia przybiera postać:

  \[ R=\begin{bmatrix} a & b & c \\\\ d & e & f \\\\ g & h & 1 \end{bmatrix} \]

  Macierz ta zawiera 8 niezależnych parametrów. Do ich określenia potrzebna jest znajomość współrzędnych czterech odpowiadających sobie punktów.

💥 Zadanie do wykonania 💥

• Pobierz udostępniony obraz.

• Bazując na kodzie dla przekształcenia perspektywicznego oraz przykładzie obsługi myszki, napisz program, który:

  • wczytuje udostępniony obraz drogi,
  • umożliwia wybór czterech punktów (w ramach testów proszę klikać w kolejne narożniki jezdni),
  • wykonuje przekształcenie perspektywiczne w celu “wyprostowania” jej.

Histogramy

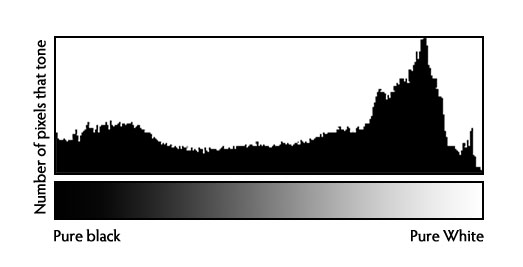
Histogram obrazuje liczebność poszczególnych wartości jasności pikseli na obrazie. W przypadku obrazu w skali szarości możliwy jest podział na maksimum 256 przedziałów (każdy o szerokości 1) lub mniejszą liczbę, w której każda grupuje pewien zbiór wartości (dla 4 przedziałów będą to wartości 0 - 63, 64 - 127, 128 - 191, 192 - 255). Przykładowy histogram (pochodzi ze strony):

💥 Zadanie do wykonania 💥

Zapoznaj się z histogramami w opencv https://docs.opencv.org/5.x/d1/db7/tutorial_py_histogram_begins.html, a następnie wykonaj kroki:

• Wyświetl histogram dla swojego obrazu, zarówno w skali szarości, jak i dla obrazu kolorowego.

Uwaga:
Do wyznaczania histogramu użyć funkcji OpenCV - cv2.calcHist, natomiast do wyświetlania bibliotekę matplotlib.

• Wykonaj operację wyrównania histogramu (do fragmentu CLAHE (Contrast Limited Adaptive Histogram Equalization)) opisaną w: https://docs.opencv.org/5.x/d5/daf/tutorial_py_histogram_equalization.html.

Zadania do samodzielnej realizacji

💥 Zadanie do wykonania 💥

Napisz program, który umożliwia zaznaczenie dwóch punktów (będzie to lewy górny róg i prawy dolny pewnego obszaru) i wykonanie w tym fragmencie obrazu operacji progowania dla kanału G (zielonego).

💥 Zadanie do wykonania 💥

Napisaz program, który po wskazaniu przez użytkownika czterech punktów na obrazie docelowym wklei w niego drugi obraz tak, aby wskazane punkty określały jego narożniki (celem jest zastąpienie jednego z obrazów wiszących w galerii sztuki obrazem mopsa).

Uwaga:
Zadanie może wymagać dodawania obrazów z maską (bitwise operation).